Visuele test: hoeveel driehoeken tel je? De meeste mensen die het proberen hebben een verkeerd aantal

Als je dit artikel hebt geopend, is dat omdat je zin hebt om jezelf te testen met een logisch spel of raadsel. Welnu, wat je op deze pagina vindt, lijkt misschien heel eenvoudig, aan de andere kant is wat je wordt gevraagd te doen heel eenvoudig, oftewel tellen! Wie kan er niet tellen? Wacht echter om dit te zeggen. In feite vragen we je om aan te geven hoeveel driehoeken je kunt tellen in de figuur van het spel. Ben je klaar om jezelf te testen? Laten we beginnen!
Visuele test: Hoeveel driehoeken zijn er in totaal?
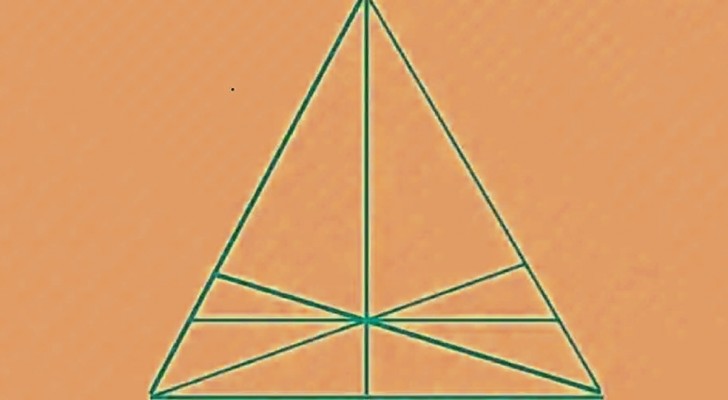
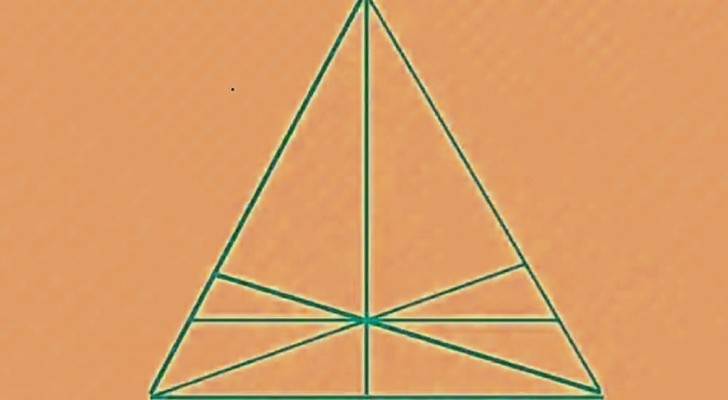
De afbeelding van het raadsel die we je vandaag aanbieden is heel eenvoudig: het is een driehoek, gelijkzijdig om precies te zijn - als je nog herinneringen hebt aan je schooltijd! - waarin zich verschillende andere driehoeken bevinden. De figuur is symmetrisch, dus het zou voldoende zijn om de helft van de driehoeken te tellen en het resultaat te verdubbelen om de uiteindelijke oplossing te krijgen. Maar let op! Mensen die dit spel spelen, hebben het eindresultaat vaak verkeerd door een vergissing.
De oplossing van het spel: zoveel driehoeken zijn er...

Neem de tijd en zorg ervoor dat het precies de juiste veronderstelling is. Daarna ben je klaar om te verifiëren dat de oplossing die je voorstelt ook daadwerkelijk de juiste is! De uiteindelijke oplossing is 23! Is dat het getal dat je dacht? Als dit niet het geval is, vertellen wij je waarom de uiteindelijke oplossing 23 is: laten we eerst de helft van de grootste driehoek bekijken: binnenin bevinden zich 8 driehoeken, waarbij ook de driehoeken worden meegerekend die worden gevormd door de vereniging van twee driehoeken. Dit getal 8 moet met 2 worden vermenigvuldigd omdat, zoals we al zeiden, de figuur symmetrisch is. Vervolgens bekijken we de figuur als geheel en tellen we vervolgens de driehoeken die worden gevormd door de vereniging van de linkerhelft en de rechterhelft. Zo kom je op 22.
En waar is de laatste driehoek? Veel mensen vergeten de hoofddriehoek te tellen, de grootste, de gelijkzijdige driehoek die alle andere kleinere driehoeken bevat. Dus hier komen we bij het eindresultaat.
Dit spel had gemakkelijk kunnen zijn, maar het brengt veel mensen in de problemen! Dit soort spelletjes en raadsels verbergen altijd een moeilijkheid die ervoor zorgt dat mensen een verkeerde oplossing geven.





